東京大学大学院工学系研究科 教授 浅見泰司先生インタビュー「空間関係・統計的性質を保持しつつ空間的個体特定化危険を回避するための空間情報安全化処理方法の開発」（第2回）
離散データと連続データ、1次元データと多次元データについて、それぞれの違いを教えてください。
離散データとは、たとえば人数や商品数のように整数で表現されるデータのことです。つまり「１」の次が「１．１」ではなく「２」になる、小数点を含まないデータのことです。一方連続データとは、「１」の次が「１．１」、その次が「１．１１」「１．１１１」…となるような、データとデータの間を無限に量ることができるデータのことです。
１次元データと多次元データの違いは、学校で行われるテストを例に考えると、「１科目のみで評価するテスト」が１次元データ、「２科目以上の科目で総合的に評価するテスト」が多次元データです。
そこで本研究では、Negative Surveyを多次元データにも適用できる手法を確立しました。
下の図を見てください。「本当の答え」は「※」のブロックです。しかし回答者が白色のブロックを同じ確率で回答しても、図のような数式によって、解析者は「※」の値を統計的に復元することできます。これがSelective Negative Surveyです。
１次元データと多次元データの違いは、学校で行われるテストを例に考えると、「１科目のみで評価するテスト」が１次元データ、「２科目以上の科目で総合的に評価するテスト」が多次元データです。
そこで本研究では、Negative Surveyを多次元データにも適用できる手法を確立しました。
下の図を見てください。「本当の答え」は「※」のブロックです。しかし回答者が白色のブロックを同じ確率で回答しても、図のような数式によって、解析者は「※」の値を統計的に復元することできます。これがSelective Negative Surveyです。
この方法なら、多次元データであっても選択肢が３つ以上あれば、Negative Surveyが使えるのですね。「ＡとＢのどちらを選ぶか」といった二者択一の調査では、データを曖昧にすることはできないのでしょうか。
二者択一の場合は、Negative SurveyにRandomized Responseを組み合わせた方法を用います。
たとえば「コンビニで万引きをしたことがあるか？」という質問をしたとき、答えは「万引きしたことがある」「万引きしたことがない」の２つしかありません。そしてこれは、回答者にとって抵抗感が強い質問です。
調査の目的が「万引きの経験があるのは誰か」ではなく「このクラスで何割の生徒が万引きした経験があるのか」を知ることであれば、次のような方法があります。
回答者は答える前に、調査者に見えないようにコイントスを行い、「表が出たら必ず『万引きしたことがある』と答える。裏が出たら正直に答える」というルールに従ってもらいます。調査者はコイントスの結果が分からないので「万引きしたことがある」という回答が、コイントスの結果なのか正直に答えているのか分かりません。つまり収集したデータは曖昧なものになります。
たとえば「コンビニで万引きをしたことがあるか？」という質問をしたとき、答えは「万引きしたことがある」「万引きしたことがない」の２つしかありません。そしてこれは、回答者にとって抵抗感が強い質問です。
調査の目的が「万引きの経験があるのは誰か」ではなく「このクラスで何割の生徒が万引きした経験があるのか」を知ることであれば、次のような方法があります。
回答者は答える前に、調査者に見えないようにコイントスを行い、「表が出たら必ず『万引きしたことがある』と答える。裏が出たら正直に答える」というルールに従ってもらいます。調査者はコイントスの結果が分からないので「万引きしたことがある」という回答が、コイントスの結果なのか正直に答えているのか分かりません。つまり収集したデータは曖昧なものになります。
コイントスをして表が出るか裏が出るかは五分五分の確率ですから、実際に万引きをしていなくても、５０％の確率で「万引きしたことがある」と答えることになります。
そうです。つまり、
【万引きしたことがある＋コイントスで表が出た→Ａ】
【万引きしたことがある＋コイントスで裏が出た→Ｂ】
【万引きしたことがない＋コイントスで表が出た→Ｃ】
【万引きしたことがない＋コイントスで裏が出た→Ｄ】
とすると、この調査の回答は、
「万引きしたことがある」→Ａ＋Ｂ＋Ｃ
「万引きしたことがない」→Ｄ
になります。
コイントスで表・裏が出る確率は５０％なので、ＡとＢ、ＤとＣの値は同じです。
つまり「万引きしたことがある」の回答率から「万引きしたことがない」の回答率を差し引くことで「本当に万引きをしたことがある人」の割合を算出することができます。
もっと分かりやすく言えば、この集団は「万引き経験がある人」と「万引き経験がない人」から構成されているため、片方の数値が分かれば、自動的にもう片方の数値も判明します。
実際に万引きをしたことがない人の割合をｐとすると、「万引きしたことがない」と回答した人の割合は０．５ｐです。その回答率を２倍して、１００％から差し引けば、実際に万引きした人の割合を算出できるのです。
【万引きしたことがある＋コイントスで表が出た→Ａ】
【万引きしたことがある＋コイントスで裏が出た→Ｂ】
【万引きしたことがない＋コイントスで表が出た→Ｃ】
【万引きしたことがない＋コイントスで裏が出た→Ｄ】
とすると、この調査の回答は、
「万引きしたことがある」→Ａ＋Ｂ＋Ｃ
「万引きしたことがない」→Ｄ
になります。
コイントスで表・裏が出る確率は５０％なので、ＡとＢ、ＤとＣの値は同じです。
つまり「万引きしたことがある」の回答率から「万引きしたことがない」の回答率を差し引くことで「本当に万引きをしたことがある人」の割合を算出することができます。
もっと分かりやすく言えば、この集団は「万引き経験がある人」と「万引き経験がない人」から構成されているため、片方の数値が分かれば、自動的にもう片方の数値も判明します。
実際に万引きをしたことがない人の割合をｐとすると、「万引きしたことがない」と回答した人の割合は０．５ｐです。その回答率を２倍して、１００％から差し引けば、実際に万引きした人の割合を算出できるのです。
確率が分かっているランダム要素を入れることで、収集時のデータが曖昧でも、最終的に目的の比率は算出できるということですね。
この方法をさらに進化させて、多次元かつ連続データの場合と、二者択一型の質問を含む離散データの場合に攪乱が可能なMNS-RRT（multidimensional Negative Surveys with Randomized Response Technique）を新たに確立しました。回答者にとって言いたくないことを言わせずに、求める比率を出すことができるため、センシティブな内容の調査であってもデータを集めやすくなるはずです。
ありがとうございました。それではふたつめの「秘密分散を用いた秘匿演算方式の開発」について、教えていただけますか。
まず、秘密分散法についてご説明します。
たとえばインターネットで商品を購入するときにはキャッシュカードの番号を、銀行ＡＴＭでお金を引き落とすときには暗証番号を打ち込みますが、それらはすべて暗号化されてネットワークに流れ、認識されています。
秘密分散法は、このような重要な情報を任意のｎ個に分割して暗号化する方法です。分割した情報は任意のｋ個集めなければ、データを復号できません。つまり第三者にネットワークをハッキングされても、分割した情報１つだけでは復号できないため、高い安全性を得ることができるのです。
次に、秘匿演算方式について。
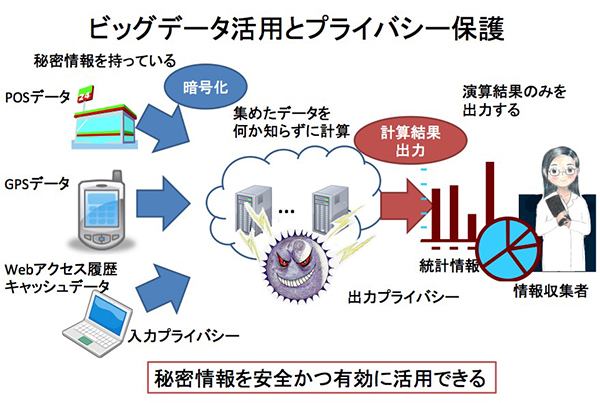
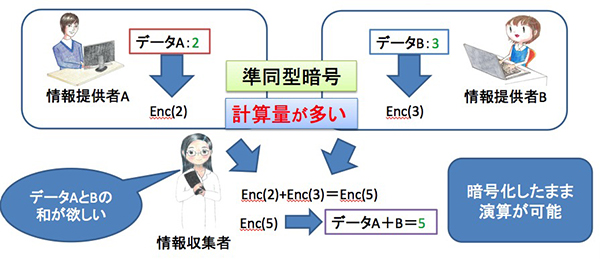
従来の技術では、暗号化したデータに対して何らかの統計を求める場合、一度データを復号する必要がありました。しかし復号した時点で、安全性は低下します。この課題に対して生まれたのが、暗号化した状態で さまざまな演算を可能にする技術です。これを準同型暗号といいますが、秘密分散法もその1つです。
たとえばインターネットで商品を購入するときにはキャッシュカードの番号を、銀行ＡＴＭでお金を引き落とすときには暗証番号を打ち込みますが、それらはすべて暗号化されてネットワークに流れ、認識されています。
秘密分散法は、このような重要な情報を任意のｎ個に分割して暗号化する方法です。分割した情報は任意のｋ個集めなければ、データを復号できません。つまり第三者にネットワークをハッキングされても、分割した情報１つだけでは復号できないため、高い安全性を得ることができるのです。
次に、秘匿演算方式について。
従来の技術では、暗号化したデータに対して何らかの統計を求める場合、一度データを復号する必要がありました。しかし復号した時点で、安全性は低下します。この課題に対して生まれたのが、暗号化した状態で さまざまな演算を可能にする技術です。これを準同型暗号といいますが、秘密分散法もその1つです。
復号して演算をするのではなく、暗号化したままのデータで、加算値や乗算値などの演算ができるのですか。
そうです。データの復号を一度も行わないため、情報収集者にも解析者にも個々の値は分かりませんが、目的の演算結果は得ることができます。つまり準同型暗号を効率的に利用することができれば、ビッグデータの活用とプライバシーの保護を両立させることができるのです。
ただし、課題もあります。一般に準同型暗号は計算量が多いという問題がありますが、秘密分散法は比較的処理が軽く実用的です。しかし、分割・暗号化されたデータはオリジナルデータよりもサイズが大きくなってしまうという問題が発生します。
ただし、課題もあります。一般に準同型暗号は計算量が多いという問題がありますが、秘密分散法は比較的処理が軽く実用的です。しかし、分割・暗号化されたデータはオリジナルデータよりもサイズが大きくなってしまうという問題が発生します。
