人体内部の電気特性の画像化についても、お話を伺いたいと思います。

がん組織は健常組織と電気的な特性が大きく異なるため、体内の電気特性がわかれば診断に役立ちます。しかし、人体内部の電気特性を直接計測する方法はまだ確立しているとはいえません。

そこで私は近年、計測可能なデータから数理的に体内の電気特性を求めることに取り組んできました。そのなかで、複素関数論において、ある領域の境界線上の関数の値から領域内部の関数の値を求める「コーシーの積分公式」を応用することを思いつきました。「領域の境界」とはまさに体表であり、体表ならば電気特性の計測は容易です。この発想を元に、「MRIで計測した磁場と体表の電気特性を入力するだけで、内部の任意点における電気特性を求められる再構成公式（観測データから逆問題の解を直接導く公式）」を得ました。

ただし、複素関数論は2次元でしか成り立ちません。そこで、アナロジー的に3次元化を行って任意点における計算式を導出し、さらにこれまで必要だった境界上の電気特性を不要にする手法を開発した上で、シミュレーションや模擬生体において導電率の画像化に成功しました。今回、脳腫瘍の境界が明瞭に画像化されることを確かめ、さらに人体のデータへの適用も進めています。

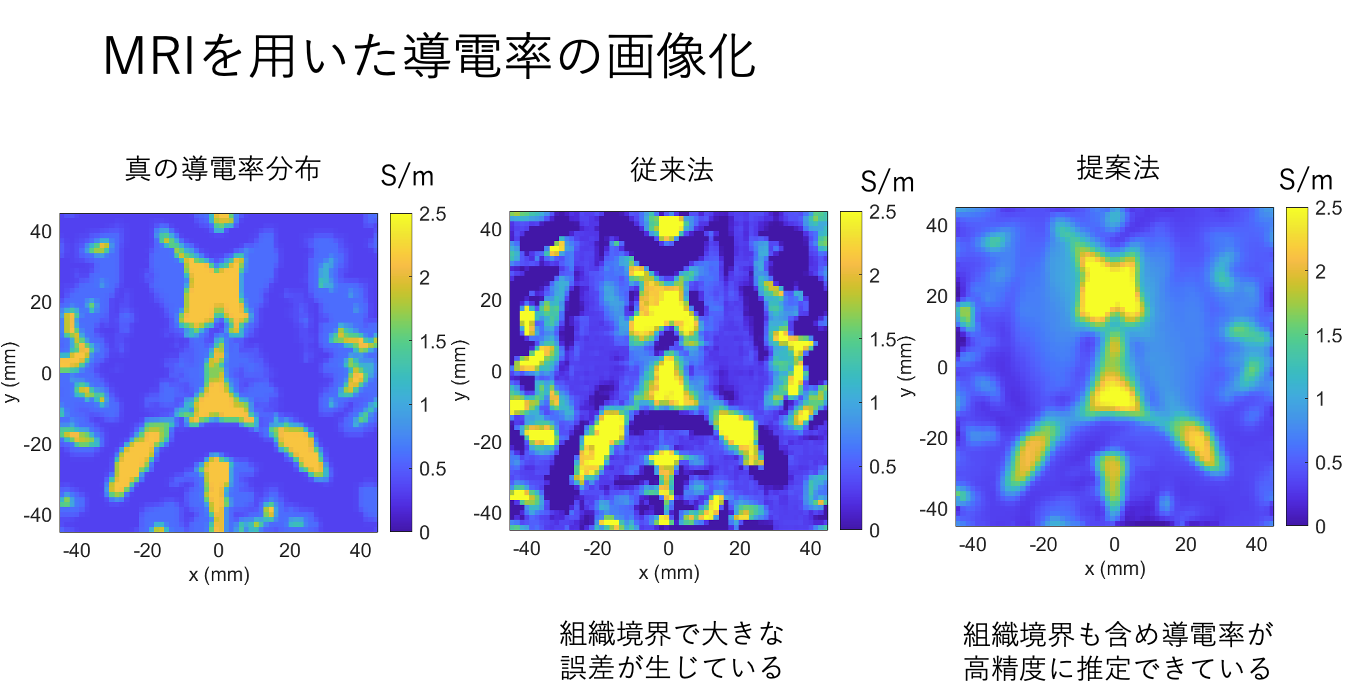磁場データから導電率分布を復元するシミュレーション。従来法では、導電率が変化する境界付近で青色が濃く誤差が大きいが、提案法の結果は真の導電率分布とよく一致している

かなり実用化に近づいているのですね。それでは次に、非破壊検査への応用についても教えてください。

今回の対象は、棒状鉄鋼製品です。欠陥がある製品に磁場をかけると、磁束が欠陥部分にぶつかって漏れてくるため、漏洩磁束から欠陥の有無と位置を推定します。従来は多数のセンサを円周上に並べてスキャンする方法がとられていますが、センサの素子数に分解能が左右されることと、多数の素子の調整が煩雑なことが問題です。

脳磁場逆問題と非破壊検査法の開発は一見全く異なる分野であるが、観測した磁場から内部構造を推定するという点で、非常に近いテーマ

どのようにアプローチされたのでしょうか。

まず、漏洩磁束の観測データから欠陥位置を推定する直接再構成公式を導出しました。式を見ると、漏洩磁束密度B（棒の周方向の角度φの関数）とcosφの積を円周に沿って積分した値と、Bとsinφの積を同様に積分した値によって決まることがわかります。このように、関数にcos関数あるいはsin関数をかけて積分した量を、フーリエ係数と呼びます。

本研究で得られた、欠陥位置の直接再構成公式

欠陥位置の特定には、このフーリエ係数の値が必要なのですね。

はい。そして通常こうした積分量を計測するには、円周上にセンサを並べ、計測された磁場の荷重和をとってフーリエ係数を近似的に計算します。しかし、それでは多数のセンサが必要となり先に述べた課題の解決にはなりません。

そこで今回、2個のセンサだけでフーリエ係数を直接計測できるコイルを発案しました。丸棒の表面に導線を8の字状に2周させており、1周目と2周目の間隔がcos係数で変化します。コイルの各点では、その位置における磁束密度と導線間隔の積が検出されます。コイルは棒の表面を一周しますから、その積は円周に沿って積分され、結果として、フーリエ係数そのものを出力する１個のセンサになるのです。

これを90度回転させたコイルがsin係数の項に対応します。両方のコイルを1つのパイプに巻き、パイプ内に検査対象の棒を走らせれば、欠陥の向きが決定できます。棒の表面に這わせるようにコイルを巻いているところも今回のポイントで、センサ感度を増加させ微小な傷に対応可能にしています。

開発したコイル（上）と、鉄鋼棒材を使ったデモンストレーション（下）。2つのセンサの出力が、2色の波形で表示される