木造建物のねじれ振動の研究をしているなかで、この現象に気づきました。

近年、多くの戸建て住宅にソーラーパネルが乗っています。日当たりの良い南側にパネルを置くと、南側が重くなります。また、南側は日当たりが良いので大きな窓をつけます。すると、壁が少なくて重いという、ねじれやすい条件が整うのです。過去の大きな地震においても、戸建て住宅がねじれるように倒壊してしまう現象が多く発生しています。

ところが、さまざまな文献を調べているとき、海外の木造中層建物の実験事例で、対称な形状でバランスがよいにもかかわらず、なぜかねじり振動が発生する、という報告が目に留まりました。

建築分野では、P-Δ効果という現象が知られています。これは、鉛直方向の力（P）に、水平方向の変位（Δ）が加わると、建物を転倒させる向きに力のモーメントが生じるというものです。そこに着想を得て「建物に水平方向の力を加えると、ねじれが生じるのではないか」と考えたことが、そもそもの始まりです。

その後、研究を進める中で、2方向に硬さが違う物体を水平方向に変形させると、釣り合いを保つために「ねじれのトルク」が生まれることが、ねじれが発生する本当の理由であり、Q-Δ効果の本質であることが明らかになりました。

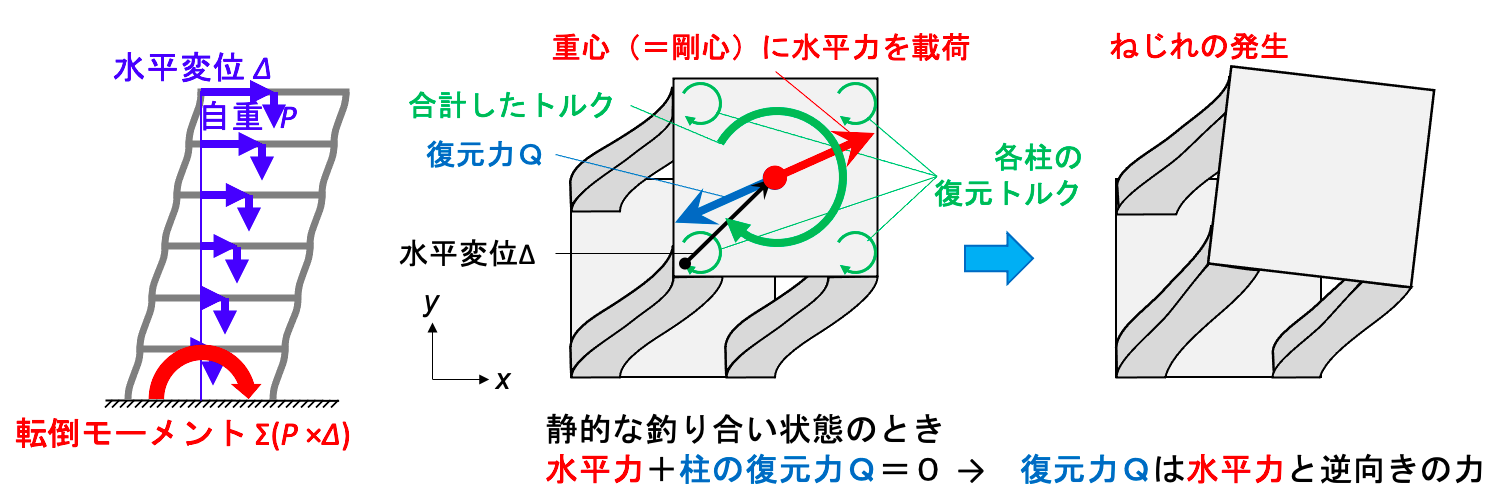
Q-Δ効果の着想のきっかけとなったP-Δ効果と、その後明らかになったQ-Δ効果の概念図。二方向の硬さの違いが、ねじれ振動を生み出すことが明らかになった

一層モデルの運動方程式は、下図のようになります。着目すべきは、ねじれ（θ）の釣り合いを表す式に、x方向の変形とy方向の変形の積（xy）が現れることです。つまり、水平方向の変位が、ねじれの力を生み出しているのです。

x方向の固有振動数（＝固有周期の逆数）で揺れる変位x、y方向の固有振動数で揺れる変位yの積を、三角関数の積和の公式を用いて変形すると、x方向の固有振動数とy方向の固有振動数の和の振動数を持つトルクと、差の振動数を持つトルクの、二つの重ね合わせで表現できることがわかります。このどちらかのトルクの振動数が建物のねじり振動の固有振動数と一致すると、建物がぐんぐんねじれる。これがQ-Δ共振の正体であることがわかりました。

一層モデルの運動方程式。今まで知られていなかった、地震の際に発生するトルクを数式化することに成功した

その通りです。建物が正方形の断面で2方向が同じ周期で揺れる場合にはQ-Δ共振は起こりませんが、多くの超高層建物は長方形の断面をしており、長辺方向と短辺方向の固有振動数が異なるため、Q-Δ共振が起こる可能性があります。

これまでは、L字形の建物や、片方だけが重かったり壁がなかったりする建物は、バランスが悪いせいでねじれる振動が生まれると考えられてきました。そのため耐震設計においては、バランスの良さを基準にした安全性のチェックも行われています。

ところが本研究により、バランスの良い建物でもねじれるという、新しい共振メカニズムが明らかになりました。これはいわば耐震設計の盲点であり、この現象について把握するだけでなく、設計法や耐震改修法の開発までつなげる必要があると考えています。

現象の理論化には、学生との協力も必須。お互いにアイディアを出しながら、理論をブラッシュアップしていく